Holografía y Matemática
DOI:
https://doi.org/10.36790/epistemus.v18i37.367Palabras clave:
Holograma, luz láser , ecuación de onda, solución de Kirchhoff, fase estacionariaResumen
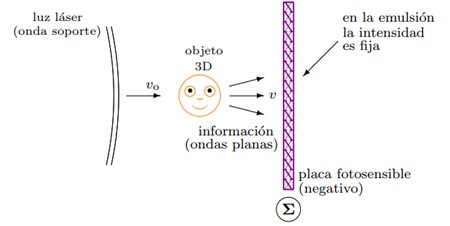
El objetivo general de este escrito es analizar matemáticamente el proceso físico de reproducción de un holograma de transmisión, con el fin de contrastar resultados directamente observables respecto a aproximaciones obtenidas de forma teórica. Por una parte, al observar un holograma se localiza sobre este una región en la que se reproduce fielmente un objeto tridimensional impreso con una técnica fotográfica especial llamada holografía. Por otra parte, al aplicar un modelo matemático simple para describir este hecho, por medio de la conocida ecuación de onda clásica —con solución dada en forma de Kirchhoff, la cual se analiza con un método asintótico de análisis complejo— se obtiene un resultado aproximado que permite realizar una conclusión congruente sobre este proceso particular.
Descargas
Citas
[[1] P.R. Garabedian. Partial Differential Equations. Chelsea Publishing Co., 1986. DOI: https://doi.org/10.1016/B978-0-12-044375-8.50016-2
G. Saxby. Practical Holography. Boca Raton, Florida: IoP Publishing, 2004.
Disponible en https://doi.org/10.1201/9781420033663 DOI: https://doi.org/10.1201/9781420033663
H.M. Smith. Principles of Holography. Nueva York: John Wiley & Sons, 1979.
R. Flores-Espinoza y R. González-González. Temas y Problemas Selectos de Análisis Matemático. Teoremas de Existencia y Aplicaciones. Hermosillo, Sonora: Universidad de Sonora, 2022.
Disponible en https://doi.org/10.47807/UNISON.95 DOI: https://doi.org/10.47807/UNISON.95
J.E. Marsden. Elementary Classical Analysis. San Francisco: W.H Freeman and Company, 1974.
M.G. García y R. González-González. Notas de Cálculo Vectorial. Hermosillo, Sonora: Universidad de Sonora, 2019.
Disponible en https://www.mat.uson.mx/sitio/documentos/libros/Notas_Calculo_Vectorial.pdf
G.B. Arfken. Mathematical Methods for Physicists, 3.a ed. Orlando: Academic Press,1985.
Disponible en https://doi.org/10.1016/C2013-0-10310-8 DOI: https://doi.org/10.1016/C2013-0-10310-8
R. Courant y D. Hilbert. Methods of Mathematical Physics: Vol. II. Partial Differential Equations. Interscience Publishers, 1965.
J.W. Dettman. Applied Complex Variables. Nueva York: Dover Publications, 1984.
A. Erdelyi. Asymptotic Expansions. Dover Publications, 1956. DOI: https://doi.org/10.21236/AD0055660
B. Friedman. Lectures on Applications-Oriented Mathematics. Nueva York: John Wiley & Sons, 1991. DOI: https://doi.org/10.1002/9781118033111
J.P. Keener. Principles of Applied Mathematics. Transformation and Approximation.
Addison-Wesley, 1988.
Disponible en https://doi.org/10.2307/3618500 DOI: https://doi.org/10.2307/3618500
E. Mihaylova. Holography–Basic Principles and Contemporary Applications.
InTech DTP, 2013.
Disponible en http://dx.doi.org/10.5772/46111 DOI: https://doi.org/10.5772/46111
I. Stakgold. Green's Functions and Boundary Value Problems. Nueva York: John Wiley & Sons, 1979.
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2025 EPISTEMUS

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-CompartirIgual 4.0.
La revista adquiere los derechos patrimoniales de los artículos sólo para difusión sin ningún fin de lucro, sin menoscabo de los propios derechos de autoría.
Los autores son los legítimos titulares de los derechos de propiedad intelectual de sus respectivos artículos, y en tal calidad, al enviar sus textos expresan su deseo de colaborar con la Revista Epistemus, editada semestralmente por la Universidad de Sonora.
Por lo anterior, de manera libre, voluntaria y a título gratuito, una vez aceptado el artículo para su publicación, ceden sus derechos a la Universidad de Sonora para que la Universidad de Sonora edite, publique, distribuya y ponga a disposición a través de intranets, internet o CD dicha obra, sin limitación alguna de forma o tiempo, siempre y cuando sea sin fines de lucro y con la obligación expresa de respetar y mencionar el crédito que corresponde a los autores en cualquier utilización que se haga del mismo.
Queda entendido que esta autorización no es una cesión o transmisión de alguno de sus derechos patrimoniales en favor de la mencionada institución. La UniSon le garantiza el derecho de reproducir la contribución por cualquier medio en el cual usted sea el autor, sujeto a que se otorgue el crédito correspondiente a la publicación original de la contribución en Epistemus.
Salvo indicación contraria, todos los contenidos de la edición electrónica se distribuyen bajo una licencia de uso y Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0) Puede consultar desde aquí la versión informativa y el texto legal de la licencia. Esta circunstancia ha de hacerse constar expresamente de esta forma cuando sea necesario.